Understanding and Calculating Standard Error
Introduction
The standard error (SE) is a critical concept in statistics, particularly when it comes to understanding the reliability and accuracy of sample data. It provides a measure of how much a sample mean is expected to vary from the true population mean. This blog post will guide you through the concept of standard error, its calculation, and its significance, using clear explanations backed by recent academic resources.
What is Standard Error?
In simple terms, the standard error is a measure of the variability or dispersion of sample means around the population mean. It’s a way to quantify how much we can expect a sample statistic (like the sample mean) to differ from the population parameter (like the population mean).
The smaller the standard error, the more representative the sample is of the population. Conversely, a larger standard error indicates greater variability among sample means, suggesting that the sample might not be as accurate a reflection of the population.
Importance of Standard Error
Understanding and calculating the standard error is crucial in various fields, including economics, psychology, medicine, and social sciences, where researchers often work with sample data rather than entire populations. The standard error helps in:
1-Estimating Confidence Intervals:
Confidence intervals rely on the standard error to determine the range within which we expect the true population mean to lie. A smaller standard error results in a narrower confidence interval, indicating a more precise estimate.
2-Hypothesis Testing:
In hypothesis testing, the standard error is used to calculate test statistics like the t-score, which determines whether to reject the null hypothesis. It plays a vital role in determining the statistical significance of research findings.
3-Assessing Sampling Methods:
The standard error can provide insights into the effectiveness of the sampling method used. A large standard error might suggest that the sample is not random or that the sample size is too small.
How to Calculate Standard Error
The standard error can be calculated using the following formula:
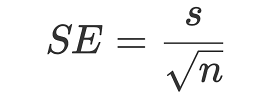
Where:
- s is the sample standard deviation.
- n is the sample size.
Let’s break this down:
Sample Standard Deviation (s): This measures the amount of variability in the sample data. It’s calculated by taking the square root of the variance (the average of the squared differences from the mean).
Sample Size (n): This refers to the number of observations in the sample. The larger the sample size, the smaller the standard error, assuming the sample standard deviation remains constant.
Example Calculation
Imagine you have a sample of 50 students' test scores with a sample standard deviation of 10. To calculate the standard error::
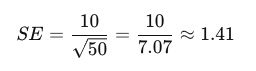
This means that the sample mean is expected to vary by approximately 1.41 points from the true population mean.
Reducing Standard Error
To reduce the standard error, you can either increase the sample size or reduce the sample variability. Increasing the sample size has a more significant impact because the sample size is under the square root in the denominator, making it a powerful tool in reducing standard error.
Conclusion
The standard error is an essential statistical tool that helps researchers understand the accuracy and reliability of their sample data. By calculating the standard error, researchers can make informed decisions about their data, estimate population parameters more precisely, and conduct more reliable hypothesis tests.
Understanding how to calculate and interpret the standard error is crucial for anyone working with sample data. It allows for more accurate and meaningful insights, ultimately leading to better decision-making based on statistical analyses.
References
Gelman, A., Hill, J., & Vehtari, A. (2022). Regression and Other Stories. Cambridge University Press.
Smith, M. S. (2023). Statistical Analysis: A Comprehensive Introduction. Wiley.
Thompson, B. (2023). Modern Data Analysis: Statistical Tools and Applications. Springer.
Xu, Y., & Zhao, J. (2022). Applied Statistical Methods: Practical Approach and Applications. Routledge.